論文のためのグラフ作成と結果・考察の書き方:散布図
論文やレポートを書いていて、最もよく使うグラフの一つが散布図です。今回の記事では、どんなときに散布図を描くのか、散布図は論文中でどのように説明すれば良いのか、そして散布図をもとにどんなことが考察できるのか、などについて解説していきます。
散布図を使うのはどんなとき?
散布図を使うのは、二つの変量の関係を調べたいときです。例えば、身長と体重の関係や、年齢と体力スコアの関係などです。
二つの変量とも、数量データ(比例尺度・間隔尺度)または順序尺度である必要があります。順序尺度とは、例えばアンケート回答の満足度(5:とても満足、4:満足、3:普通、2:不満、1:とても不満、など)のようなものです。「はい・いいえ」「ある・ない」「男性・女性」のような名義尺度は大小関係がないので、散布図を作成することはできません。
散布図では、横軸を説明変数(独立変数)、縦軸を目的変数(従属変数)とします。例えば、「身長が変われば体重も変わるのではないか」と考えているとすれば、身長が横軸、体重が縦軸になります。「年齢によって体力が変わるのではないか」と考えているとすれば、年齢が横軸、体力が縦軸になります。これを逆にすると、「体力が変われば、年齢も変わるのではないか」というおかしな論理になってしまいます。縦軸と横軸の関係を間違えると回帰分析の結果も変わってくるので、慣れていない方は注意してください。
なお、二変量のうちどちらが説明変数でどちらが目的変数なのか、はっきりしないこともあります。これは二変量がほぼ対等な関係にある場合で、例えばA地点とB地点の気温の関係や、商品Aと商品Bの満足度の関係を表す場合です。こういうときは、説明変数・目的変数という概念は捨てて、単純にどちらかを横軸、もう一方を縦軸に選べば良いでしょう。ただし、二つの変量が本当に対等な関係にあるのかどうかは十分に考える必要があります。
統計解析
散布図を作成してデータの分布を見ると、増加傾向や減少傾向が見えることがあります。そんなときは、その傾向を統計学的に解析してみましょう。散布図のデータ傾向を解析するにはさまざまな方法がありますが、ここでは最もよく使われる単回帰分析とスピアマンの順位相関分析だけを挙げておきます。
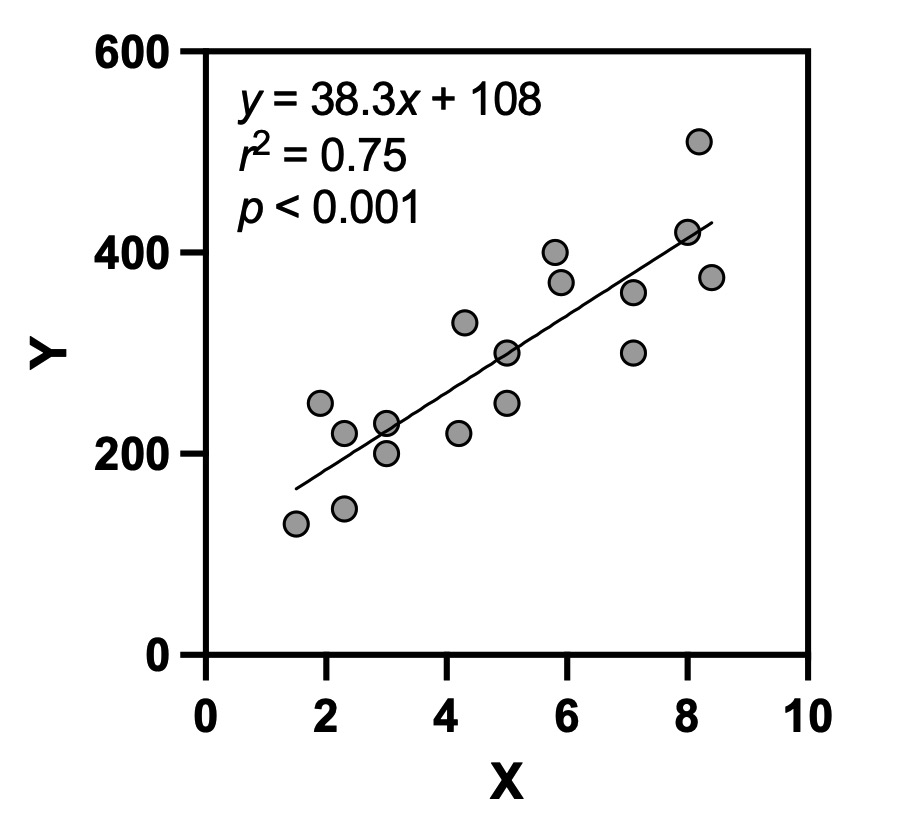
単回帰分析はいわゆる直線回帰のことで、二変量の関係が直線関係にあるときに行います。説明変数も目的変数も連続データである必要があり、順序尺度については単回帰分析を行うことはできません。また、厳密には残差の正規性や等分散性が求められますが、実際にはそこまで確認せずに回帰分析を行っている事例も多くあります。図1が単回帰分析の例です。
データの分布が増加傾向あるいは減少傾向を示しているものの、直線的な傾向ではない場合、スピアマンの順位相関分析を行います。あるいは、単回帰分析の前提条件(残差の正規性や等分散性など)を満たしていない場合もスピアマンの順位相関分析です。これはいわゆるノンパラメトリックな手法で、データ数値そのものではなく、数値を順位に変換して分布の傾向を評価します。そのため、アンケート調査で得られる「満足度」のような順序尺度にも用いることができます。
単回帰分析やスピアマンの順位相関分析を行うと、データ分布の増加傾向あるいは減少傾向を統計学的に示すことができます。
結果の書き方
散布図を作成して統計解析を行なった後は、その結果について文章で記述していきます。結果の書き方はさまざまですが、例えば次のように書くことができます。
単回帰分析の場合
Aが増加するにつれて、Bは直線的に増加した。
スピアマン順位相関分析の場合
Cが増加するにつれて、Dも増加する傾向が見られた。
スピアマンの順位相関分析では、数値を順位に変換して解析しているため、「直線的」という表現が使えるかどうかは慎重に判断したほうが良いでしょう。特に目的変数や説明変数が順序尺度の場合は、軸の目盛りが等間隔とは言えないので、「直線的」という表現は適切ではありません。
考察の書き方
論文の「考察」では、散布図で見られた傾向や統計解析の結果をもとに、それが何を意味しているのか解釈していきます。上の図1の例を使えば、
「XとYの間には有意な正の相関が見られたことから、XがYに影響を与えている可能性がある」
のように解釈することができます。ここで注意しなければならないのは、散布図の結果だけをもとにして、「AがBに影響を与えている」と断定してはいけないということです。回帰分析にしても順位相関分析にしても(そしてそれ以外の統計解析でも)、データに相関や関連性があるからといって、因果関係があるとは限らないからです。そのため、上の例文でも「可能性がある」と書きました。
もちろん、散布図だけでなく、それ以外のデータも総合的に加味しながら、最終的に「影響を与えている」と結論づけることは、論文著者の主張としては問題ありません。(そう言い切れるだけの自信があれば、の話ですが。)
結果の解釈としては、「XがYに影響を与えている可能性がある」となりますが、それで終わってしまっては考察として非常に物足りないものになってしまいます。どういう理由や過程でそうなっているのか、なぜその理由や過程を考えるのかなど、散布図の解釈から言えることを膨らませていきます。この辺りについては、以前に書いたこちらの記事をご覧ください。
まとめ
今回は論文・レポートを想定した散布図の使い方についてまとめました。棒グラフと並んで、論文・レポートでは最もよく使われる図の一つなので、基本的な解析方法や説明の仕方はぜひ身に付けておきましょう。次回は棒グラフについてまとめます。

この記事を書いた人
田中泰章
Yasuaki Tanaka
プロフィール
自然の仕組みや環境問題、社会・教育制度などについて広い視点から考える自然科学者。2008年に東京大学大学院で博士号(環境学)を取得した後、東京大学、琉球大学、米国オハイオ州立大学、ブルネイ大学など、国内外の大学で研究と教育に約15年間携わってきました。これまでに30報以上の学術論文を筆頭著者として執筆し、国際的な科学雑誌の査読者として多数の論文審査も行っています。大学教員としては、これまでに40名以上の学生(学部・修士・博士を含む)を研究指導し、若手研究者を育成してきました。専門は「人間と自然とのかかわり」で、人間活動が自然界に与える影響を生物学・化学・社会学などの複合的な視点から研究しています。




