単回帰分析の基本:エクセル出力結果の見方と論文での書き方
「統計解析」と聞いて、多くの方が思い浮かべるのが単回帰分析、いわゆる直線回帰ではないでしょうか。今回の記事では、単回帰分析をエクセルで実行したときに出力される結果の見方や、論文での書き方などについて解説していきます。
単回帰分析の前に
単回帰分析は直線回帰と呼ばれることもあり、その名の通り、直線で二変量の関係を表したいときに行います。関係性に注目したい2つの変量がある場合、まずは散布図を描いてみて、直線関係が見られるかどうか確認しましょう。
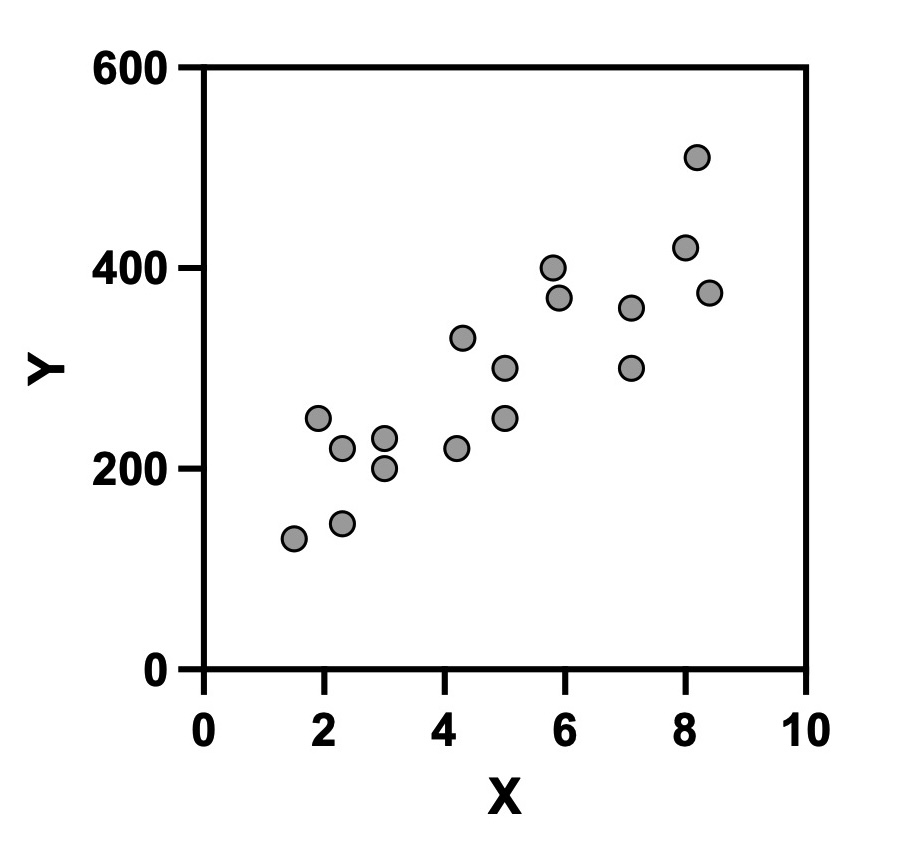
図1 XとYの関係を表す散布図
この段階で、もし2つの変量(XとY)が直線関係にない場合(例えば、指数関数的に増加・減少していたり、放物線を描いていたりする場合)、直線を当てはめるのは不自然ですので、単回帰分析を行うのは適切ではありません。データを変換して(例えば対数変換など)、プロットが直線的に分布する状態になれば単回帰分析を行うことができます。
分析結果の見方
図1のデータについて、エクセルで単回帰分析を行ったときの出力結果(表1)と、回帰直線を引いたグラフ(図2)を示します。
表1 エクセルで回帰分析を行ったときの出力結果
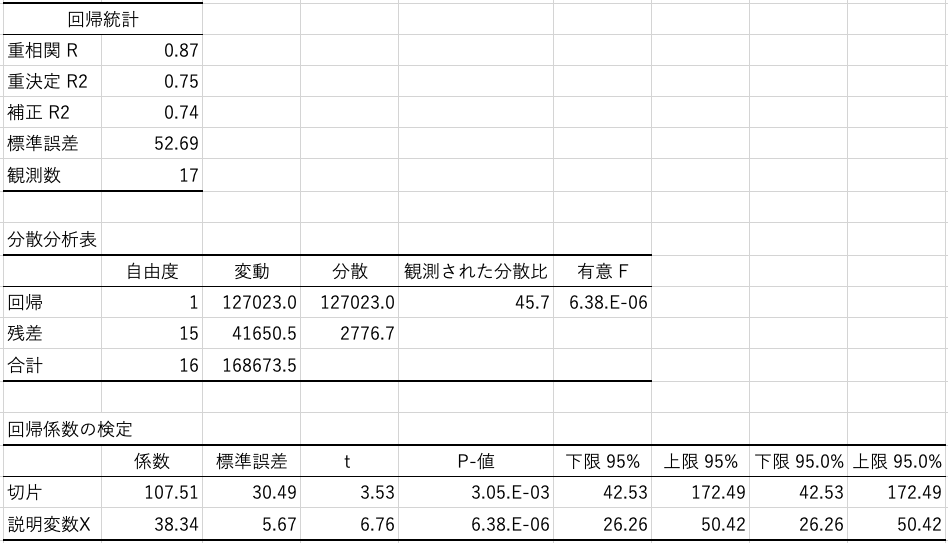
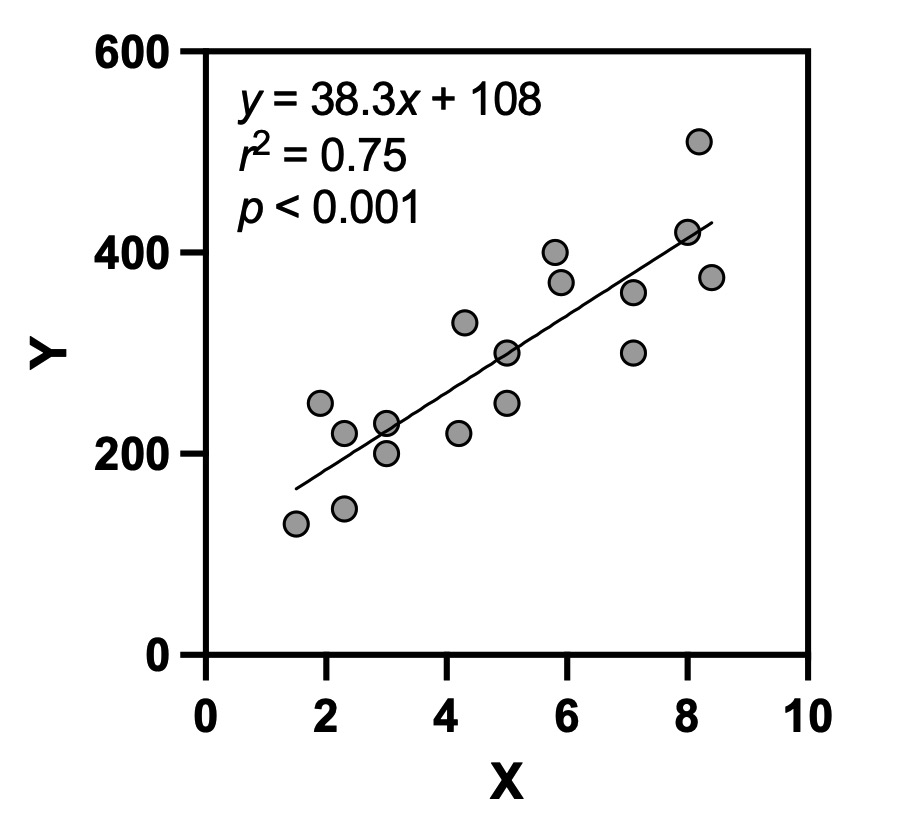
図3 散布図と回帰直線
表2 相関係数が示す相関関係の目安
| 相関係数 | 相関関係 |
|---|---|
| 0 〜 ±0.2 | ほとんど相関がない |
| ±0.2 〜 ±0.4 | やや相関がある |
| ±0.4 〜 ±0.7 | 相関がある |
| ±0.7 〜 ±0.9 | 強い相関がある |
| ±0.9 〜 ±1.0 | 非常に強い相関がある |
表1の「回帰統計」には相関関係の強さが示されていて、相関係数が大きければ回帰直線はデータによく当てはまっており、小さければあまり当てはまっていないと判断されます。今回の場合は相関係数r=0.87ですので、「強い相関がある」と言えます(表2)。
表1の「分散分析表」を見ると、「自由度」「変動」「分散」などが書かれていますが、最も注目したいのは「有意F」です。これはF検定の結果を示していて、いわゆる有意水準(p値)のことです。一般的には、p<0.05であれば有意と判断され、回帰によって求められた式が役に立つということになります。言い換えれば、説明変数Xが目的変数Yの予測に役立つということです。これ以降でも、有意水準を5%として話を進めていきます。
「分散分析表」の下には、回帰係数の有意性と信頼区間が示されています。ここでは特に、「係数」と「p値」に注目します。表中の「係数」とは、回帰直線をy=ax+bとしたときのaとb、つまり傾きと切片に該当するものです。今回のケースでは、切片が107.5、傾きが38.3となり、回帰式はy=38.3x+108と書くことができます(図2)。
そして「p値」は、それらの係数が意味のあるものかどうかを判定したものです。切片のp値が0.05未満であれば、切片は0ではない可能性が高い、つまり切片に意味があるということです。逆に切片のp値が0.05以上であれば、切片は0の可能性がある(切片の値に意味はない)ということになります。
説明変数Xについても同様です。説明変数Xのp値が0.05未満であれば、傾きは0ではない可能性が高い、つまり傾きに意味があるということです。逆に説明変数のp値が0.05以上であれば、傾きは0の可能性がある、つまり説明変数と目的変数に関連性はないということになります。
切片にしても傾きにしても、p値が0.05以上の場合、表に示されている95%信頼区間が0をまたぐことになります。このことからも、それらの係数が0の可能性があるということが分かります。
回帰分析の前提条件
ここまで、回帰式が役に立つかどうかや、切片や傾きが意味のあるものかどうかについて見てきましたが、ここで回帰分析の前提条件についても触れておきます。回帰分析(単回帰分析および重回帰分析)では、データに次のような条件が求められます。
- 独立性
- 等分散性
- 正規性
- 線形性
詳細は別記事でまとめたいと思いますが、ここで注意したいのは、正規性や等分散性、独立性などの条件は、データそのものではなく、残差についての条件ということです。データ自体は正規分布している必要も、等分散である必要もありません。
回帰式の有意性(分散分析表)や回帰係数の有意性は、いずれも残差の正規性や等分散性を前提として計算されているものですので、表中のp値や95%信頼区間を採用するためには、これらの条件を満たしているか確認しておく必要があります。
解析結果の説明方法
単回帰分析は二変量の関係を調べるための解析ですので、その結果を論文やレポートで説明するときは、2つの変量の間に有意な関連性が見られたかどうかということが一番のポイントになります。回帰式が有意なとき、典型的な説明文は以下のようなものです。
- (説明変数)と(目的変数)の間には、有意な関連性が見られた。
- (説明変数)と(目的変数)の間には、有意な正(負)の相関が見られた。
有意であることを示すために、回帰式のp値を文末にカッコ書きで入れると良いでしょう。p値だけでなく、回帰式や決定係数を入れても良いと思います。
- (説明変数)と(目的変数)の間には、有意な関連性が見られた(p<0.001)。
- (説明変数)と(目的変数)の間には、有意な正の相関が見られた(y=38.3x+108、r2=0.75、p<0.001)。
解析結果の解釈(考察)
研究論文では、結果をもとに考察を書いていきます。結果を解釈しながら、研究の結論を出すために議論を展開していくということです。
回帰分析を行う目的としては、単純に説明変数と目的変数の関連性を調べたい場合もあれば、説明変数が目的変数に与える影響(因果関係)を調べたい場合もあるでしょう。後者の場合は、「きっと、(説明変数)が(目的変数)の要因だろう」と想定して、回帰分析を行っているはずです。そこで、次のように単回帰分析の結果を解釈したくなるかもしれません。
(説明変数)と(目的変数)の間には有意な関連性が見られたことから、(説明変数)が(目的変数)に影響を与えていることが明らかになった。
しかしながら、上のように解釈するのは誤りです。回帰分析というのは基本的に二つの変量の関係性を示すだけで、因果関係を示しているわけではないからです。
単回帰分析で有意な関連性が見られた場合、次のように解釈するのが適切です。
(説明変数)と(目的変数)の間には、有意な正(負)の相関が見られた。これは、(説明変数)が(目的変数)に影響を与えていることを示唆する。
一文目が結果、二文目が結果の解釈です。「影響を与えていることを示唆する」の部分は、「要因である可能性を示している」など、他の表現でも大丈夫です。大切なことは、回帰分析だけで因果関係を証明することはできず、回帰分析から言えるのはあくまで「要因である可能性」や、「影響を与えている可能性」に過ぎないということです。
そのため、この「可能性」を少しでも高められるように、自分の主張や論理を組み立てていきます。例えば、その「可能性」を裏付けるような他の結果に言及したり、同様の相関関係が示されている先行研究に言及したりします。そうやって、「(説明変数)が(目的変数)の要因である可能性が極めて高い」と読者に思わせられるように、考察を展開していきます。
まとめ
単回帰分析について、出力結果の読み取り方、前提条件、記述方法などをまとめました。実際の分析作業では前提条件を最初にチェックするので、以下のような流れになります。
- 回帰分析の前提条件を満たすかどうかチェックする。
- 分散分析表のp値から、回帰式の有意性を判定する。
- 回帰係数とそのp値から、回帰係数の有意性を判定する。
回帰式が有意でも、言えるのはあくまで2つの変量の「関連性」であり、「因果関係ではない」という点にご注意ください。

この記事を書いた人
田中泰章
Yasuaki Tanaka
プロフィール
自然の仕組みや環境問題、社会・教育制度などについて広い視点から考える自然科学者。2008年に東京大学大学院で博士号(環境学)を取得した後、東京大学、琉球大学、米国オハイオ州立大学、ブルネイ大学など、国内外の大学で研究と教育に約15年間携わってきました。これまでに30報以上の学術論文を筆頭著者として執筆し、国際的な科学雑誌の査読者として多数の論文審査も行っています。大学教員としては、これまでに40名以上の学生(学部・修士・博士を含む)を研究指導し、若手研究者を育成してきました。専門は「人間と自然とのかかわり」で、人間活動が自然界に与える影響を生物学・化学・社会学などの複合的な視点から研究しています。



