量的データを解析する基本的な手順
今回の記事では、量的データの基本的な解析手順についてまとめたいと思います。これからデータをエクセルに入力して統計解析しようとしている方は、ぜひ参考にしてみてください。
①一変量の分布
データ解析で最初に行うのは、調査項目それぞれのデータ分布を確認することです。通常、研究データとして得られる数値は一つや二つではなく、数百から数千、ときにはそれ以上に及びます。そんなたくさんの数字を単に眺めていても、なかなかデータの全体像はつかめません。全体像をイメージしやすくするために、データを「要約する」必要があるわけです。
データの分布を確認する方法はデータの種類によって異なるので、まずはデータの種類について整理しておきます。
数量データとは?
「体重」「身長」「速度」「本数」「温度」など、多くの計測データが該当します。例えば1メートルの棒が2本で2メートル(1+1=2)、2メートルの棒が10本で20メートル(2×10=20)というように、加減乗除できるデータです。
厳密には、数量データは「間隔尺度」と「比例尺度」に分けられますが、統計解析を行う上での扱い方はほとんど同じなので、ここではまとめて「数量データ」と呼ぶことにします。
順序尺度とは?
順序尺度とは、「満足度」や「理解度」のように、大小や順位を表す数値データです。ただし、数量データと異なり、数値の間隔に意味はない(等間隔性が保証されていない)ので、加減乗除できません。
名義尺度とは?
名前や性別、色など、数値で示すことができないデータです。ただし、統計解析をするために、ダミー変数を使って便宜的に数値化することはあります。
データの種類(数量データ、順序尺度、名義尺度)についてはこちらの記事をご覧ください。
データの分布を確認する方法は、大きく次のように分けることができます。
数量データの場合
数量データの分布を確認するには、基本統計量を計算します。基本統計量とは、最大値や最小値、中央値、平均値、標準偏差など、データ分布の特徴を示す数値です。エクセルの「データ分析」機能を使うと、次のような項目をすぐに計算してくれます。
- 平均
- 標準誤差
- 中央値 (メジアン)
- 最頻値 (モード)
- 標準偏差
- 分散
- 尖度
- 歪度
- 範囲
- 最小
- 最大
- 合計
- 標本数
最頻値や分散、四分位点など、いろいろな統計量がありますが、とりあえず最初に挙げた5項目(最大値や最小値、中央値、平均値、標準偏差)を計算、チェックするだけでも十分だと思います。
例えば、ある測定値について、AグループとBグループを比較しようとしているなら、それぞれのグループの平均値と標準偏差(データのばらつき)を見るだけで、どちらが高そうか簡単に分かります(もちろん、断定するためには後で正確に統計解析する必要があります)。
基本統計量を計算することによって、データのおおまかな分布が分かるだけでなく、異常値や入力ミスを見つけることもできます。例えば、人間の年齢データについて基本統計量を計算してみて、最大値が「254」歳と出てきたら、「データのどこかに入力ミスがあるはず」と思いますよね。
順序尺度の場合
順序尺度のデータは、数量データと違って等間隔性が保証されていないので、平均値や標準偏差を計算することにあまり意味はありません。また、回答の選択肢が3〜5個くらいのアンケート調査だと、最大値も最小値も選択されている可能性があるため、最大値や最小値の情報も役に立ちません。
そういうデータの場合は、各順位(アンケート調査でいえば、回答選択肢の数字)の割合を計算することで、データ分布の全体像を把握します。アンケート調査の結果を使った論文では、たいていの場合、そのような回答者の割合を示す図表が掲載されているはずです。
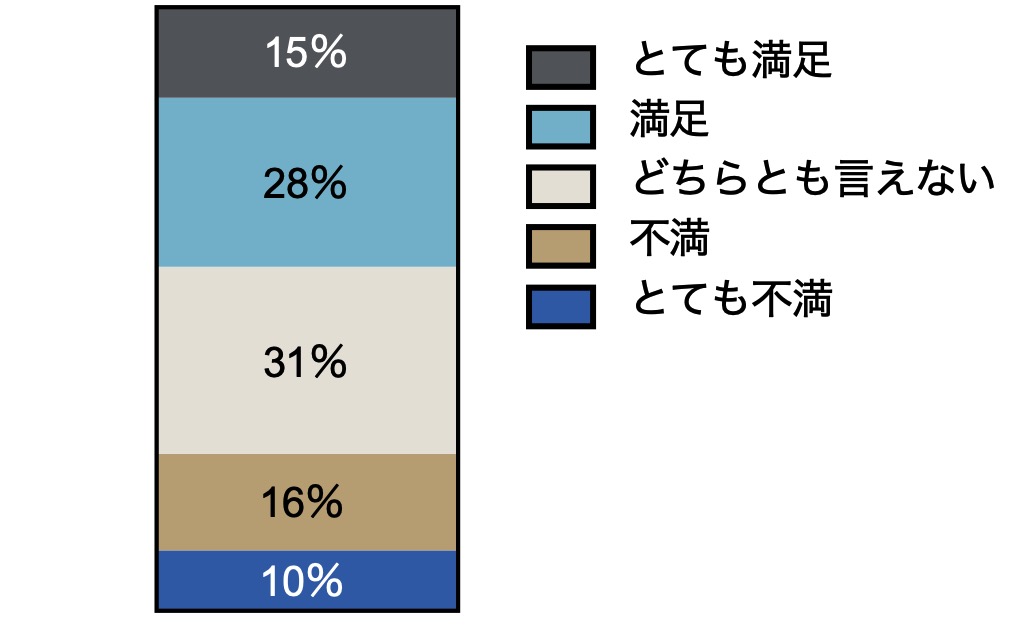
順序尺度の場合、平均値や標準偏差を計算することに「あまり意味はありません」と書きましたが、ここに「あまり」と付けたのには理由があります。理論的には意味がない(間違っている)のですが、現実的には順序尺度のデータを使って平均値や標準偏差を計算している論文は非常に多いからです。平均値や標準偏差を計算するなら、その値を示すことに本当に意味があるのかどうか、よく考えてから行うようにしましょう。
名義尺度の場合
名義尺度は数値で表すことができないため、順序尺度と同じように割合で示すのが一般的です。例えばアンケート調査であれば、選択肢の5を選んだ人が何%、4を選んだ人が何%、のようにデータを整理していきます。
②二変量の関係
一変量の分布を調べたあとは、二変量の関係に注目します。二変量の関係とは、例えば身長と体重のような、異なる二つの測定値の関係です。測定値Xが大きくなると測定値Yも大きくなるとか、逆に測定値Xが大きくなると測定値Yは小さくなるとか、そういう二つの変量の関係に注目するということです。身長と体重のように、二つの変量がともに数量データのときは、散布図を描くことによって、二つの変量の関係を簡単に視覚化できます。
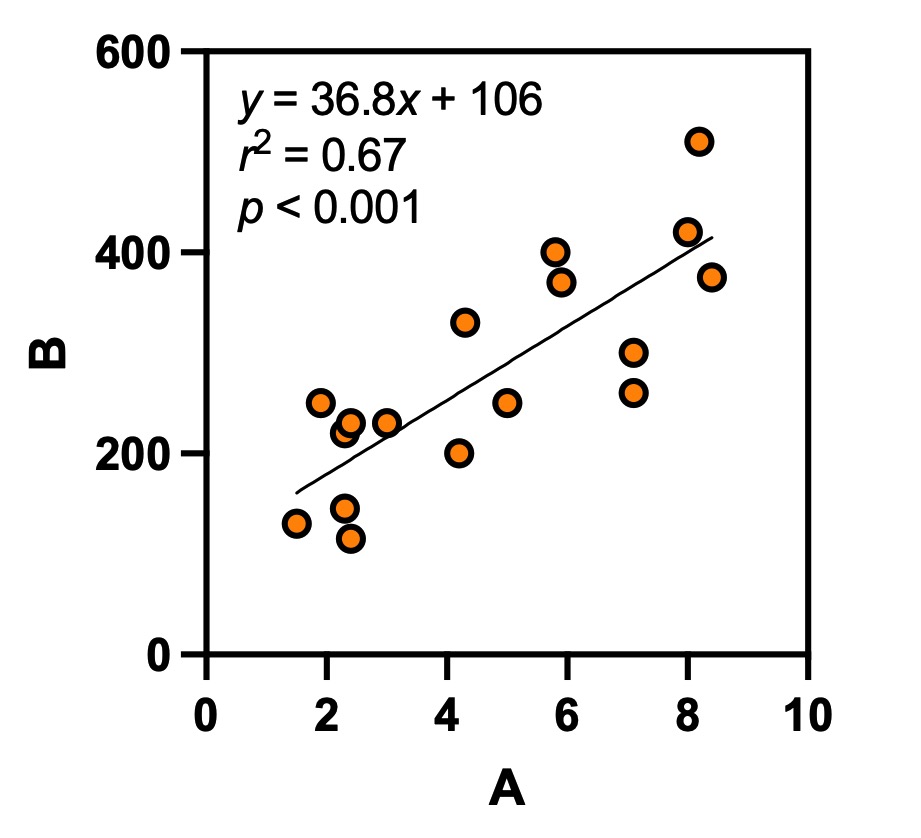
もう一つのよくあるケースは、グループ間の比較です。測定値Xについて、AグループとBグループで異なるかどうかを検討するような場合ですが、これは測定値とグループという二つの変量の関係(x軸とy軸のような、二次元で表せる関係)を調べていることになります。この場合は、グループが名義変数なので散布図を作ることはできず、横軸にグループ名を置いた棒グラフで視覚化するのが一般的です。棒グラフの長さは、その変量の平均値にするのが一般的で、標準偏差や標準誤差などのエラーバーを付けるとグループ間の差をさらにイメージしやすくなります。
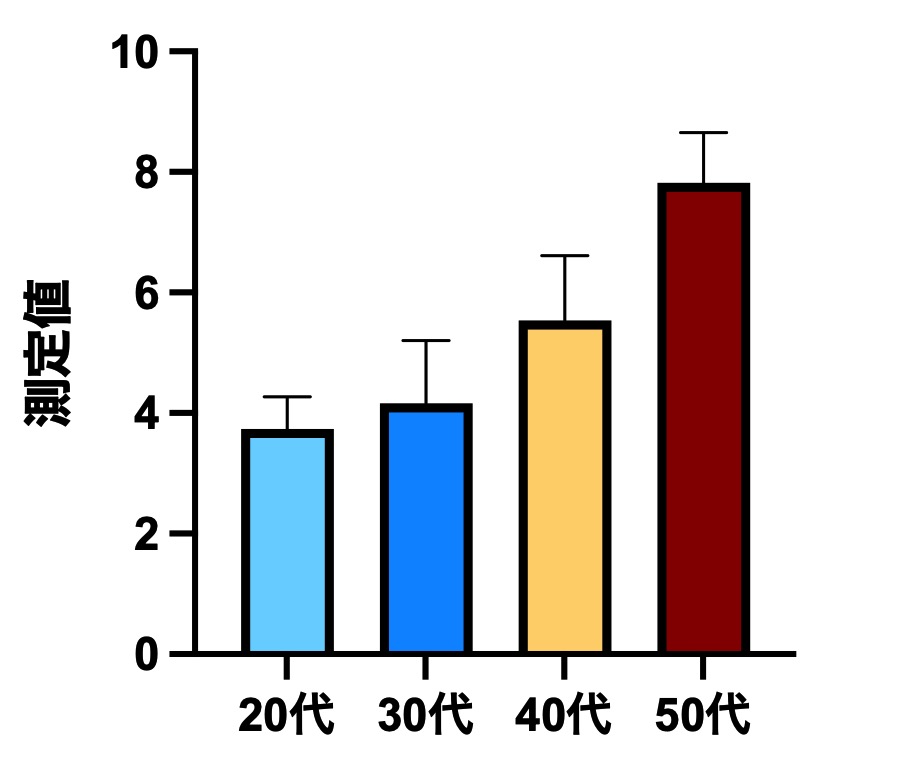
③多変量解析
二変量の関係を解析するだけでは不十分な場合、三つ以上の変量を同時に解析する、いわゆる多変量解析を考えます。有名なものとしては、主成分分析や因子分析、重回帰分析、ロジスティック回帰分析などが該当します。今回の記事はデータ解析全体の流れをまとめることを目的としているので、各解析の詳細については省略しますが、要するに複数の変量を使ってデータ全体の傾向を捉えようとする解析です。
例えば、20個の質問からなるアンケート調査を100人に実施して、その結果から回答者の特徴を知りたいような場合です。この場合、20の変量を同時に解析する必要があるので、多変量解析を行います。また、測定値Xに影響を与える可能性としてA、B、C、D、Eという5つの因子が考えられる場合、合計6つの変量を使って多変量解析を行うことになります。
このように、多変量解析は複数の変量を同時に解析するので、うまく使えばとても便利な方法です。しかしその一方で、計算方法が複雑で、結果をイメージしにくいという欠点もあります。例えば、XとYという二つの数量データの関係であれば、1つの平面(二次元)に描かれた散布図で視覚化できますが、6つの変量を使った重回帰分析は六次元となり、視覚的にイメージできるものではありません。
まずは一変量の分布や二変量の関係をしっかり確認して、データの全体像をイメージしたうえで、必要に応じて多変量解析を行うことが大切です。
まとめ
今回の記事では、データ解析の基本的な手順についてまとめてみました。
- 一変量の分布を調べる
- 二変量の関係を調べる
- (必要であれば)多変量解析を行う
研究目的にもよりますが、論文を書くのには二変量の関係を調べるだけで十分なことも多くあります。多変量解析を行うにしても、一変量の分布や二変量の関係をしっかりとイメージしたうえで行うようにしましょう。「論文添削サービス」を提供しながら多くの論文を見てきましたが、一変量の分布も二変量の関係もまったく調べず、いきなり多変量解析を実施しているケースがとても多いです。そうすると、データの細部を知らないまま、ぼんやりとした全体像を見ることになり、誤った結論を出しかねません。多変量解析の前に、まずは基本の解析から行ってみることをおすすめしています。

この記事を書いた人
田中泰章
Yasuaki Tanaka
プロフィール
自然の仕組みや環境問題、社会・教育制度などについて広い視点から考える自然科学者。2008年に東京大学大学院で博士号(環境学)を取得した後、東京大学、琉球大学、米国オハイオ州立大学、ブルネイ大学など、国内外の大学で研究と教育に約15年間携わってきました。これまでに30報以上の学術論文を筆頭著者として執筆し、国際的な科学雑誌の査読者として多数の論文審査も行っています。大学教員としては、これまでに40名以上の学生(学部・修士・博士を含む)を研究指導し、若手研究者を育成してきました。専門は「人間と自然とのかかわり」で、人間活動が自然界に与える影響を生物学・化学・社会学などの複合的な視点から研究しています。




