多項ロジスティック回帰分析の基本：データの形式、前提条件、分析結果の解釈

以前に二項ロジスティック回帰分析と順序ロジスティック回帰分析についてまとめましたが、今回は多項ロジスティック回帰分析を取り上げます。数式や細かい理論は省き、どういうデータの何を知りたいときに多項ロジスティック回帰分析を行うのか、前提条件は何か、分析結果をどのように解釈するのか、などについて解説していきます。

二項ロジスティック回帰分析の基本：データの形式、前提条件、分析結果の解釈

数式や細かい理論は省き、どういうデータの何を知りたいときに二項ロジスティック回帰分析を行うのか、前提条件は何か、分析結果をどのように解釈するのか、などについて…

アカデミックラウンジ

どういうデータ？

多項ロジスティック回帰分析は、目的変数が三つ以上の名義尺度のときに行います。名義尺度なので、正規性や等分散性などの前提条件は求められません。

説明変数は連続データ（数量データ）である必要があるので、順序尺度の場合はデータを連続データとして扱い、名義尺度の場合はダミー変数（0・1）に置き換えます。順序尺度を連続データとして扱うのは統計学的には問題がありますが、実際にはよく行われています。それが許容されるかどうかは分野によりますので、事前に調べてみてください。

何を知りたい？

下の表は、「花の種類」と「がくの長さ」について調査した結果の例を示しています（JMPのサンプルデータを改変）。花の種類は3種類、がくの長さはセンチメートル単位で入力され、全部で150行のデータです。

花の種類	がくの長さ（cm）
A種	5.1
A種	4.9
A種	4.7
（A種が続く）	（データが続く）
B種	7.0
B種	6.4
B種	6.9
（B種が続く）	（データが続く）
C種	6.3
C種	5.8
C種	7.1
（C種が続く）	（データが続く）

がくの長さだけを測って、花の種類をどれくらい正確に推定することができるか知りたいとき、花の種類を目的変数、がくの長さを説明変数とした多項ロジスティック回帰分析を行います。花の種類が3種類あるので「多項」と呼んでいますが、もし2種類なら二項のロジスティック回帰になります。

また、今回は話を単純化するために説明変数をがくの長さだけにしていますが、他の測定項目（花びらの長さや幅など）を入れることもできます。複数の測定項目（説明変数）から、結果（今回の場合は、花の種類）を推定します。

データの分布

ロジスティック回帰分析を行う前に、実測値の分布を把握しておくことをおすすめします。花の種類を横軸、がくの長さを縦軸にしてデータをプロットすると次のようになりました。

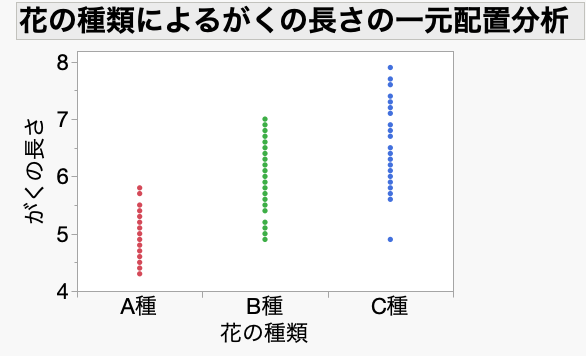
これを見ると、がくの長さはA種が一番短く、C種が一番長いことが分かります。例えば、がくの長さが4.5センチくらいのときはほぼ間違いなくA種でしょうし、7.5センチくらいあるときはほぼ間違いなくC種と言えそうです。では、6センチくらいのときはどうでしょうか？B種の可能性が高そうですが、C種の可能性もありそうですし、もしかしたらA種かもしれない、という状況ですね。

こういうときに多項ロジスティック回帰分析を行うと、A種・B種・C種である確率を計算したり、そもそもがくの長さが本当に花の種類を推定するのに有効かどうかを判断したりできます。

結果の解釈

上記の花のデータを多項ロジスティック回帰で分析した結果を示します（統計ソフトはJMPを使用）。

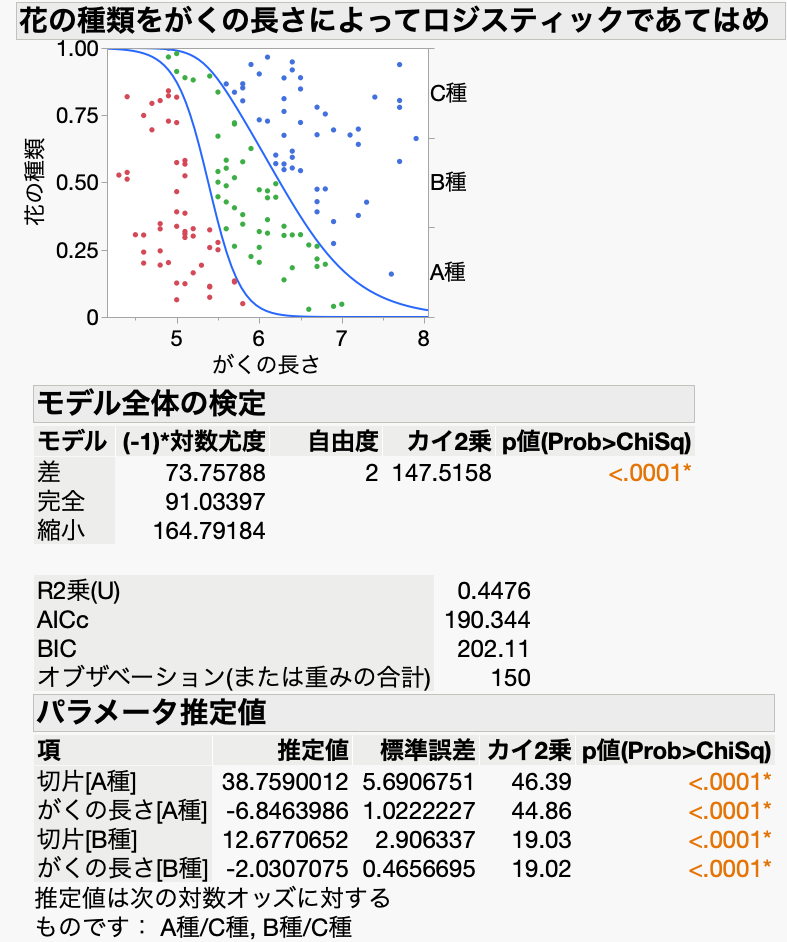
まず「モデル全体の検定」を見ると、p値が十分に小さい（<0.0001）ので、今回の回帰式が有意である、つまり目的変数を予測・説明するのに役立つと言えます。

次に「パラメータ推定値」（係数の推定値）を見ると、「がくの長さ[A種]」と「がくの長さ[B種]」のp値が0.001未満なので、これらの長さが花の種類を推測するのに有効な指標だと言えます。

そして、一番上のロジスティックプロットを見ると、がくの長さと花の種類の関係がよく分かります。たとえば、がくの長さが4.5センチくらいのときは、縦軸の0から1までが赤いプロット（A種）で占められているため、ほぼ100％の確率でA種だと言えます。また、がくの長さが7.5センチくらいのときは、縦軸の0から1までが青いプロット（C種）で占められているため、C種の可能性が高いと言えます。

では、がくの長さが6センチくらいのときはというと、最も高い可能性がB種（緑のプロット）の60％くらい、次にC種の30％くらい、A種の可能性は最も低い5％くらいであることが読み取れます。それぞれの可能性を正確に計算するためには、「パラメータ推定値」（係数）を利用します。計算の詳細は省きますが、計算するとA種：3％、B種：60％、C種：37％となりました。

まとめ

多項ロジスティック回帰分析は、目的変数が三つ以上の名義尺度のときに行います。二項ロジスティック回帰分析に比べて解析結果の解釈が複雑ですが、ロジスティックプロットを見れば、説明変数と目的変数の関係をイメージしやすいと思います。今回は説明変数が一つだけのケースを取り上げましたが、複数あっても考え方は同じなので、同じような形式のデータを持っている方は試してみてください。

また、目的変数が順序尺度のときは順序ロジスティック回帰分析を行うことができますので、こちらの記事をご覧ください。

順序ロジスティック回帰分析の基本：データの形式、前提条件、分析結果の解釈

数式や細かい理論は省き、どういうデータの何を知りたいときに順序ロジスティック回帰分析を行うのか、前提条件は何か、分析結果をどのように解釈するのか、などについて…

アカデミックラウンジ

アカデミックラウンジでは、
論文の作成やデータ解析、
研究計画などに関する
ご相談を承っております。

サービス案内