二元配置分散分析の基本を解説:出力結果の見方と論文での書き方
今回の記事では、二元配置の分散分析について解説します。二元配置の分散分析(two-way ANOVA)は、一元配置の分散分析(one-way ANOVA)と同様に非常に多くの場面で使える方法です。実際の解析結果や論文での書き方を解説していきますので、ぜひ参考にしてみてください。
どんなデータに使える?
二元配置の分散分析を行うのは、ある結果について「AとBの二つの要因が関係しているかもしれない」のような仮説を立てたときです。例えば、身長や体重などの身体的なデータであれば、年齢・性別という属性条件によって変わることが予想されます。また、植物や微生物の成長速度であれば、温度・湿度という環境条件によって変わってくるでしょう。
3つ以上の要因を考慮したいこともありますが、考慮する要因の数が増えると解析結果が複雑になり、解釈しにくくなります。そのため、一元配置の分散分析(1つの要因に注目)、または二元配置の分散分析(2つの要因に注目)が最もよく利用されます。
ここでは話を分かりやすくするために「要因」という言葉を使いましたが、分散分析で因果関係を証明できるとは限りません。研究デザインによっては因果関係を証明するような二元配置分散分析も可能ですが、基本的には分散分析で検証しているのはあくまで数値の関連性に過ぎないということに注意しましょう。この辺りについては過去記事でも解説しています。
データの準備
二元配置分散分析のサンプルデータとして、今回は表1のようなデータを想定してみます。「グループ1」と「グループ2」という2つのグループについて、3つの「条件A・B・C」で分類して、ある測定値をまとめたものです。
「グループ」としては、例えば性別や年代、居住地などの属性でも良いですし、実験区・対照区のような操作上の分類、開始時・終了時のような時間的分類も可能です。また、表では「条件」としましたが、実験や調査のために意図的に設けたような条件だけでなく、「グループ」と同じような単なる分類でも構いません。
表1 2つのグループについて、3つの条件下で得られたデータ(例)
| 条件A | 条件B | 条件C | |
|---|---|---|---|
| グループ1 | 31.5 | 55.5 | 49.5 |
| 37.5 | 54.0 | 60.0 | |
| 34.5 | 51.0 | 43.5 | |
| 30.0 | 52.5 | 48.0 | |
| 31.2 | 51.0 | 52.3 | |
| グループ2 | 39.0 | 40.5 | 40.5 |
| 28.5 | 43.5 | 39.0 | |
| 37.5 | 49.5 | 37.5 | |
| 42.0 | 42.0 | 33.0 | |
| 35.5 | 39.0 | 36.0 |
出力結果の見方
表1のデータを使って二元配置分散分析した結果を、表2に示します(統計ソフトJMPを使用)。どんな統計ソフトでも、二元配置の分散分析をすると同じような分散分析表が出力されると思います。また、データをイメージしやすいように、平均値と標準偏差のプロットを作成しました(図1)。
表2 二元配置分散分析の結果表

分散分析表(表2)には、自由度や偏差平方和、F値、p値などが要因ごとにまとめられています。
ここでの「グループ」とは、「条件」を無視したときに、グループ1とグループ2の間に有意な差が見られるかどうかという検定です。次の「条件」とは、「グループ」を無視したときに、条件A・B・Cの間に有意な差が見られるかどうかという検定です。
.jpg)
図1 グループ・条件別の平均値と標準偏差
主要因である「グループ」や「条件」に目が行きそうですが、ここで一番注目するべきポイントは「グループ*条件」、つまり「グループ」と「条件」の交互作用です。交互作用とは、2つの要因の関連性のことで、今回の例では交互作用が有意(p<0.001)なので、「グループ」間の差は「条件」によって変わることを意味します。「条件A・B・C」の効果は「グループ」によって変わるとも言え、図1を見るとその関係性がよく分かります。
つまり、「条件」を無視した「グループ」間の差(表2の「グループ」)や、「グループ」を無視した「条件」間の差(表2の「条件」)を議論してもあまり意味がないということです。
二元配置分散分析では、まずは交互作用があるかどうかに注目し、ある場合は交互作用に、ない場合は要因単独の効果に注目していきます。
分散分析の前提条件
分散分析では、回帰分析(単回帰分析および重回帰分析)と同じように、データに次のような条件が求められます。
- 独立性
- 等分散性
- 正規性
- 線形性
表1のデータについて、残差の等分散性(図2)や正規性(図3)を調べたところ問題ありませんでしたので、分散分析の結果(表2)は信用できると判断します。

図2 予測値と残差のプロット

図3 残差のQ-Qプロットと正規性の検定
多重比較検定
分散分析は、すべてのグループの平均値が同じと言えるかどうかを調べるための検定なので、どのグループ間に差があるのかまでは分かりません。具体的にどのグループ間・条件間に差があるのか調べるためには、多重比較検定を行います。今回は6つのデータ群(2グループx3条件)についてTukeyの多重比較検定を行いました。
その結果、例えばグループ1の条件Bは、グループ2の条件A・B・Cよりも値が有意に高いことや、グループ1の中では条件Aが条件B・Cに比べて有意に低いことなどが分かりました。
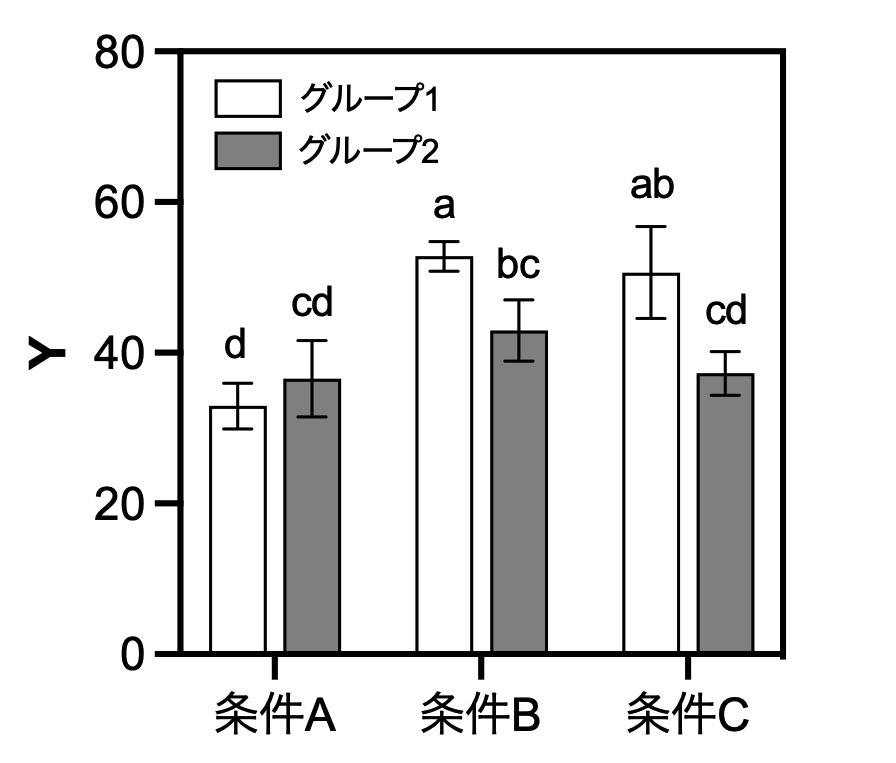
図4 多重比較検定(Tukey検定)の結果
同じ文字でつながっていないと、有意差があることを示す。
論文での書き方
二元配置分散分析の結果を論文やレポートなどに記載するときは、交互作用があるかどうかが重要なポイントになります。まず交互作用がある場合の記述例です。
分散分析の結果、「グループ」と「条件」の間には交互作用が見られた(p<0.001)。Tukey検定を行ったところ、グループ1の条件Bでは、グループ2の条件A・B・Cよりも値が有意に高かった(p<0.001)。また、グループ1の中では、条件B・Cに比べて条件Aが有意に低かった(p<0.001)。グループ1の条件Aと、グループ2の条件Aには有意な差がなかった(p=0.74)。
分散分析で有意な交互作用がない場合、「グループ」と「条件」の単独効果に注目することになります。交互作用がなかったと仮定して、記述例を書いておきます。
分散分析の結果、「グループ」と「条件」の間には交互作用が見られなかった(p=0.55)。「グループ」に注目すると、グループ1はグループ2よりも値が有意に高かった(p<0.001)。また、「条件」に注目してTukey検定を行ったところ、条件Aは条件B・Cに比べて値が有意に低かった(p<0.001)。
「グループ」は2群なので、分散分析表からどちらのグループが高いかすぐに分かりますが、「条件」は3群なので、分散分析だけではどの条件が高いのか(低いのか)分からず、何らかの多重比較検定を行う必要があります。グループ間の比較としてどういう検定を行うのかは、論文のメソッド欄にまとめて記載しておきましょう。
まとめ
以上が二元配置分散分析の基本的な流れになります。一元配置分散分析では1つの要因だけに注目すれば良いのですが、二元配置では交互作用という概念が入ってくるので、少し複雑になります。
逆に、交互作用には興味がなく、グループ間の相違だけを調べたいのであれば、二元配置分散分析を行う必要はなく、多重比較検定だけを行えば良いでしょう。
そして最後に、重要なことは分散分析表のような数字の羅列だけを眺めるのではなく、必ずグラフをチェックするということです。グラフを見ると、表からは分からないような要因同士の関係が視覚的にイメージできますので、それをしっかりと把握したうえで結果を解釈していくことが大切です。

この記事を書いた人
田中泰章
Yasuaki Tanaka
プロフィール
自然の仕組みや環境問題、社会・教育制度などについて広い視点から考える自然科学者。2008年に東京大学大学院で博士号(環境学)を取得した後、東京大学、琉球大学、米国オハイオ州立大学、ブルネイ大学など、国内外の大学で研究と教育に約15年間携わってきました。これまでに30報以上の学術論文を筆頭著者として執筆し、国際的な科学雑誌の査読者として多数の論文審査も行っています。大学教員としては、これまでに40名以上の学生(学部・修士・博士を含む)を研究指導し、若手研究者を育成してきました。専門は「人間と自然とのかかわり」で、人間活動が自然界に与える影響を生物学・化学・社会学などの複合的な視点から研究しています。




