二項ロジスティック回帰分析の基本：データの形式、前提条件、分析結果の解釈

今回は二項ロジスティック回帰分析の基本的なことをまとめます。数式や細かい理論は省き、どういうデータの何を知りたいときに二項ロジスティック回帰分析を行うのか、前提条件は何か、分析結果をどのように解釈するのか、などについて解説していきます。

ちなみに、「ロジスティック回帰分析」と言えば、この二項ロジスティック回帰分析を指すことが多いですが、多項ロジスティックや順序ロジスティックなどもあるので、ここでは「二項」を付けて表記していきます。

どういうデータ？

二項ロジスティック回帰分析は、目的変数が二者択一の名義尺度のときに行い、三択以上の名義尺度のときは多項ロジスティック回帰分析になります。二者択一の名義尺度とは、「あり・なし」「男性・女性」のように、二つのグループに分けられる指標のことです。

説明変数は連続データ（数量データ）である必要があるので、順序尺度の場合はデータを連続データとして扱い、名義尺度の場合はダミー変数（0・1）に置き換えます。順序尺度を連続データとして扱うのは統計学的には問題がありますが、実際にはよく行われています。それが許容されるかどうかは分野によりますので、事前に調べてみると良いでしょう。

何を知りたい？

下の表は、20人の被験者について、脳卒中の有無、飲酒量、喫煙状況について調査した結果です（『改訂版　すぐわかる多変量解析』より）。脳卒中は「なし：0」「あり：1」、喫煙は「吸わない：0」「少し吸う：1」「吸う：2」「よく吸う：3」として数値化してあります。

被験者	脳卒中	飲酒量	喫煙
1	1	1.3	2
2	0	0.9	0
3	1	0.7	3
4	0	0.8	0
5	1	1.7	3
6	0	1.6	3
7	0	1.0	0
8	1	1.8	3
9	0	0.7	1
10	0	0.8	1
11	1	1.3	1
12	0	1.1	0
13	1	1.0	3
14	0	1.5	0
15	0	1.6	3
16	1	1.7	2
17	0	0.9	0
18	1	1.0	2
19	1	1.9	2
20	0	1.5	1

このデータから飲酒量や喫煙が脳卒中の発生に関連しているかどうか調べたいとき、発生するかしないかは2値のデータ（0または1）なので、二項ロジスティック回帰分析を行います。

結果の解釈

上の表のデータを、統計ソフトJMPを使って二項ロジスティック回帰分析した結果を示します。

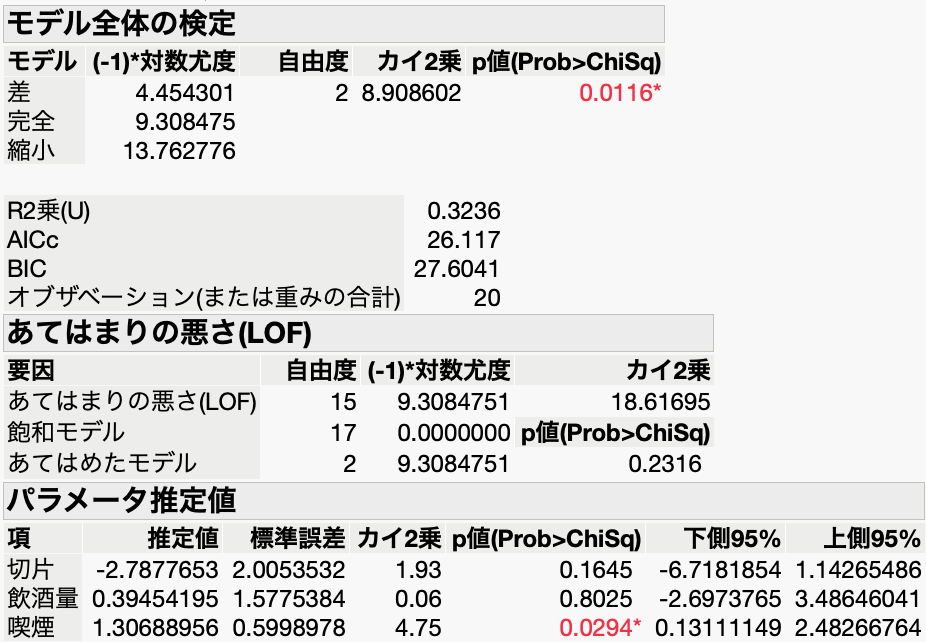
まず「モデル全体の検定」を見ると、p値が十分に小さい（<0.0001）ので、今回の回帰式が有意である、つまり目的変数を予測・説明するのに役立つと言えます。

次に「パラメータ推定値」（回帰係数の推定値）を見ると、喫煙のp値が0.05未満で有意なので、これが脳卒中の発生有無を説明するのに有効ということになります。一方で飲酒量のp値は0.80と大きいので、脳卒中の発生とは有意に関連していません。

「下限95％」「上限95％」というのは、「推定値」、つまり回帰係数の信頼区間のことです。信頼区間を見ると分かるように、回帰係数が有意（p値が0.05未満）というのは、要するに回帰係数はほぼ間違いなく正の値を取るだろう（ゼロではない）ということです。逆に、回帰係数の95％信頼区間が0をまたぎ、正の値になるか負の値になるか分からない（ゼロかもしれない）とき、有意ではないと判定されます。回帰係数がゼロなら、説明変数と目的変数の間に相関はないことになるからです。

まとめ

二項ロジスティック回帰分析は、目的変数が二値で表せる名義尺度のときに行い、目的変数に強く関連している説明変数を見つけるための解析方法です。「起こるか、起こらないか」「買うか、買わないか」「成功するか、失敗するか」のように、二つの事象の発生確率を求めたいことはよくあるので、そういうときは二項ロジスティック回帰がきっと役に立つでしょう。

アカデミックラウンジでは、
論文の作成やデータ解析、
研究計画などに関する
ご相談を承っております。

サービス案内