傾向スコアマッチング(プロペンシティスコアマッチング)の基本的な手順を解説
今回の記事では、傾向スコアマッチング(プロペンシティスコアマッチング)を取り上げたいと思います。ランダム化と同様に、バイアス(交絡因子)を除く方法としてよく利用されますので、その手順やマッチング後の解析について見ていきましょう。
どんなときに使う?
傾向スコアマッチング(法)とは、有意差を出すための統計解析ではなく、データの前処理作業のことです。傾向スコアマッチングを事前に行うことによって、集めたデータの中から有用なものだけを取り出せるので、信頼性の高い統計解析を行うことができます。
実際にどういう場合に傾向スコアマッチングを行うのか、3つの例を挙げておきます。
例)経営学分野
ある新しいシステムを導入した会社と導入していない会社について、その効果が現れたかどうかを検証したい。けれども、新システムの効果は会社の規模や業界、自己資本比率などによって変わる可能性があるので、これらのバイアスを除いて解析したい。
例)教育学分野
ある講座を受講した人と受講していない人について、その効果が現れたかどうかを検証したい。けれども、講座の効果はその人の性別や年齢、生活環境などによって変わる可能性があるので、これらのバイアスを除いて解析したい。
例)医療分野
ある薬を飲んだ人と飲んでいない人について、その効果が現れたかどうかを検証したい。けれども、薬の効果は被験者の性別や年齢、体力などによって変わる可能性があるので、これらのバイアスを除いて解析したい。
① データの準備
上記の3つの例は、次のようにまとめることができます。
傾向スコアマッチングを行うとき
Xというイベントがある場合とない場合で、効果Yが現れたかどうか検証したい。けれども、効果Yは対象者(対象物)の状況や属性など(A1、A2、A3・・・)によって変わる可能性があるので、これらのバイアスを除いて解析したい。
補足)ここでは話を分かりやすくするために「効果Y」と書きましたが、実際に検証できるのはXとYの数値としての関連性に過ぎず、Xが原因となってYが起こったという因果関係を示すものではありません。統計解析の目的としては効果を検証したいわけですが、解析結果の解釈には注意が必要です。
傾向スコアマッチングをしようと考えている方は、まずは自分が持っているデータについて、何がX、Y、A1、A2、A3・・・に該当するのか整理してみてください。
今回の記事では、ある講座を受講した人と受講していない人について、生活習慣の変化(変わった・変わらなかった)を調べたデータを想定してみます。
- A1〜A5(共変量):回答者の属性(例:性別、年齢、収入など)
- X(0または1の二値データ):講座を受講した(1)・受講していない(0)
- Y(0または1の二値データ):生活習慣が変わった(1)・変わらなかった(0)
という設定で、講座の受講と生活習慣の変化に関連性があるかどうかを判定していきます。以下のデータ表は、JMPのサンプルデータ(架空のデータ)を改変したもので、一部だけ示します。全体は181行のデータです。
| 回答者ID | A1 | A2 | A3 | A4 | A5 | X | Y |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 50 | 1 | 29.5 | 10 | 1 | 1 |
| 2 | 0 | 67 | 0 | 24 | 8 | 0 | 0 |
| 3 | 0 | 50 | 0 | 20.2 | 8 | 0 | 0 |
| 4 | 0 | 49 | 0 | 20.1 | 12 | 1 | 1 |
| 5 | 1 | 42 | 0 | 25.6 | 9 | 0 | 0 |
| 6 | 1 | 52 | 0 | 24.5 | 8 | 0 | 0 |
| 7 | 1 | 53 | 1 | 22.9 | 9 | 1 | 1 |
| 8 | 0 | 58 | 0 | 29.1 | 7 | 0 | 0 |
| 9 | 1 | 42 | 0 | 25.4 | 8 | 1 | 1 |
| 10 | 0 | 53 | 0 | 19.7 | 7 | 0 | 0 |
| (続く) |
② 要約統計量を計算する
傾向スコアマッチングをするのに必須ではありませんが、まずは各データ項目について、分布や平均値などの特徴を把握しておきましょう。図1に解析結果の例を示します。
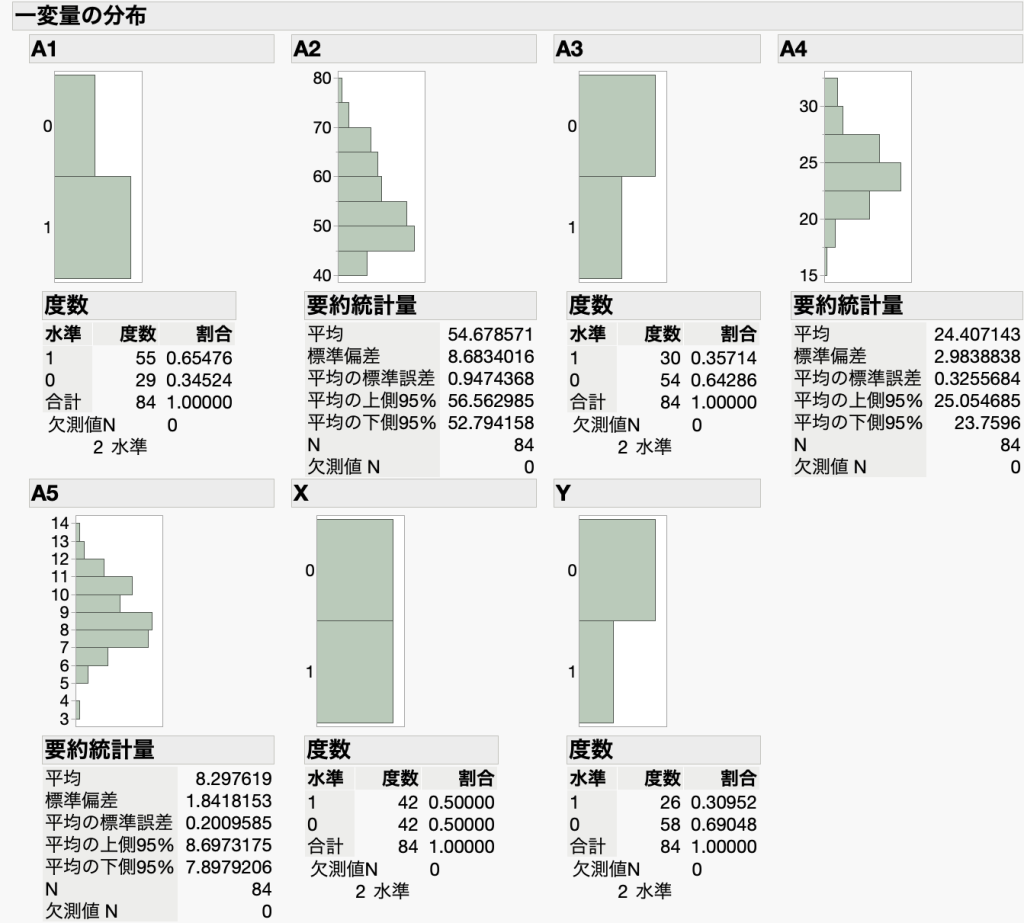
③ グループごとに指標や効果を比較する
これも必須ではありませんが、XのグループごとにYやA1〜A5(共変量)の傾向を把握しておきましょう。詳細は省きますが、グラフだけ図2に示します。
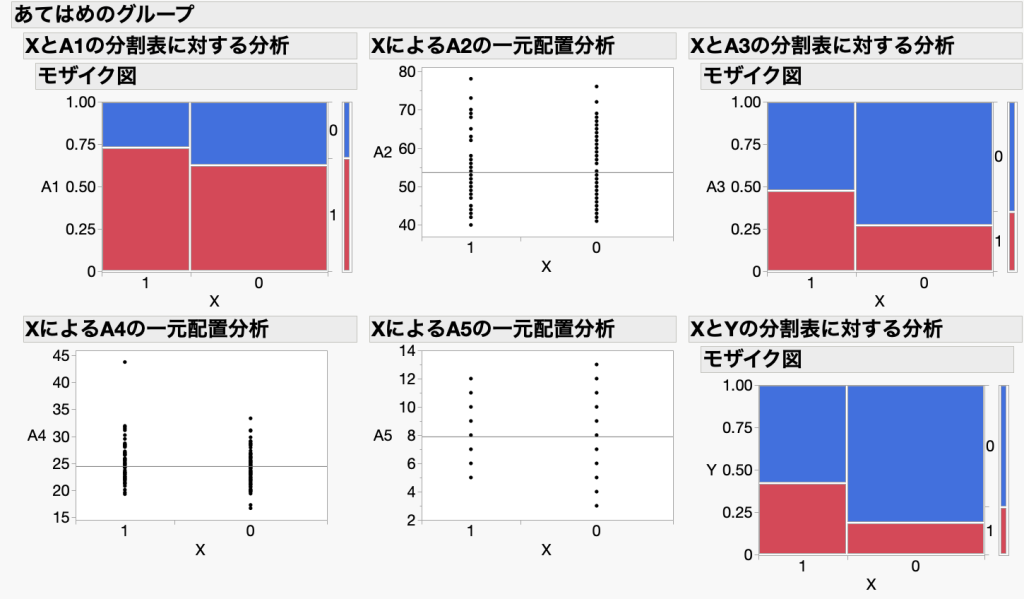
XとYの関係を見ると、Xが1の人(講座を受講した人)のほうが、Yが1(生活習慣が変わった)と答えた人の割合が高いことが分かります。しかし、現時点では回答者の属性が二つのグループ間で偏っている可能性があります。例えば、XとA3の関係を見ると、Xが1と0の人ではA3の回答傾向に明らかな偏りが見られます。そこで、XとYの関係性について信頼性を高めるために、傾向スコアを計算していきます。
④ 傾向スコアを計算する
傾向スコアを計算するには、X(0または1)を目的変数、A1〜A5を説明変数としたロジスティック回帰分析を行います。そして、A1〜A5の係数をもとに計算された、Xが1となる確率が傾向スコアになります。
傾向スコアの算出方法は統計ソフトによって異なりますが、JMPではロジスティック回帰分析の結果から、「確率の計算式の保存」を指定すると、「確率1」として傾向スコアが出力されます。
SPSSでは、ロジスティック回帰分析を実行するときに、「予測値」の「確率」にチェックを入れておけば、傾向スコアが出力されます。
⑤ マッチングする
続いて、計算された傾向スコアが近い人を二つのXグループ(講座を受講した・受講していない)から取り出し、マッチさせていきます。講座を受講したグループ、講座を受講していないグループ、それぞれからAの情報(A1〜A5)が似ている人を選んでいくということです。
マッチングの方法は統計ソフトによって異なるので、お使いの統計ソフトを確認してください。
マッチングを終えると、Aの情報(A1〜A5)が似ている人たちを分けた、二つのグループ(講座を受講した・していない)が作られます。今回のデータでは、各グループから42人ずつ、合計84人分のデータが抽出されました。全体は181人ですから、残りの97人分のデータはうまくマッチングできなかったということです。
選ばれた42人ずつのデータを使うと、二つのグループ間でA1〜A5に大きな偏りがなくなっていることが分かります(図3)。これで、回答者の属性というバイアス(A1〜A5)を除くことができました。
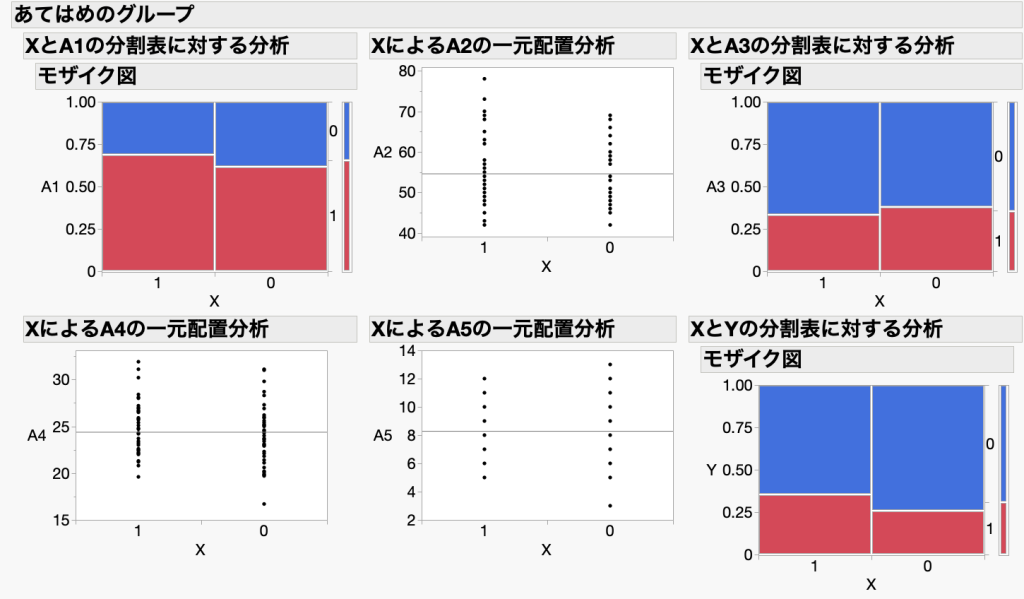
続く・・・
今回の記事では、傾向スコアマッチングはどういうときに使うのか、そしてどういう手順でマッチングさせていくのかについて解説しました。少し長くなってきたので、マッチング後の統計解析については次回の記事にまとめます。

この記事を書いた人
田中泰章
Yasuaki Tanaka
プロフィール
自然の仕組みや環境問題、社会・教育制度などについて広い視点から考える自然科学者。2008年に東京大学大学院で博士号(環境学)を取得した後、東京大学、琉球大学、米国オハイオ州立大学、ブルネイ大学など、国内外の大学で研究と教育に約15年間携わってきました。これまでに30報以上の学術論文を筆頭著者として執筆し、国際的な科学雑誌の査読者として多数の論文審査も行っています。大学教員としては、これまでに40名以上の学生(学部・修士・博士を含む)を研究指導し、若手研究者を育成してきました。専門は「人間と自然とのかかわり」で、人間活動が自然界に与える影響を生物学・化学・社会学などの複合的な視点から研究しています。



