アンケート調査結果の統計解析：質問ごとに回答結果を整理する
AcademicLounge
以前の記事で、アンケート調査を行ったときに得られるデータの種類と主な統計解析の方法についてまとめました。
基本から解説！アンケート調査結果の統計解析
アンケート調査の結果を統計解析して、「有意に・・・である」と言いたい人のための入門解説です。「こういう場合はこういう解析」という流れが分かるように解説していま…
アカデミックラウンジ 
今回からの数記事では、アンケート調査の結果を分析する実際の手順と方法について詳しく解説していきたいと思います。
最初のステップとして、今日のテーマは「質問ごとに回答結果を整理する」ということです。
調査結果を一覧表にまとめる
一般的なアンケート調査では、複数の質問（10〜30くらいの場合が多い）を最低でも数十人から数百人に聞くことが多く、その結果をまとめた一覧表（たとえばエクセル表）には多くのデータが並びます。
たとえば、回答の選択肢が1・2・3・4・5の5段階のとき、通常は次のように結果をまとめます。
| 回答者 | 質問1 | 質問2 | 質問3 | 質問4 | （続く） |
|---|---|---|---|---|---|
| 回答者A | 5 | 2 | 1 | 4 | |
| 回答者B | 3 | 3 | 2 | 4 | |
| 回答者C | 4 | 4 | 1 | 2 | |
| 回答者D | 3 | 2 | 3 | 3 | |
| （続く） |
ここでは回答者4人、質問4つだけの簡単な表を作成しましたが、実際にはもっと大きなデータセットになります。そんなデータの一覧表を見ると、どこからどう手を付ければ良いのか迷ってしまう人も多いと思います。
インターネットや本を調べると、このようなアンケート調査結果の解析方法として「多変量解析」という言葉が出てきますが、いきなり多変量解析を行うのは適切ではありません。これから説明するように、まずは質問ごとに回答結果を詳しく見ていきましょう。
質問ごとに集計表にまとめる
質問ごとに、回答結果を集計表にまとめます。人数（度数）と割合の両方をまとめるのが良いでしょう。エクセルや統計ソフトを使えば簡単に整理することができ、たとえば以下のような集計表を作成できます。
| 回答 | 人数 | 割合 |
|---|---|---|
| 1（とても不満） | 20 | 10% |
| 2（不満） | 32 | 16% |
| 3（どちらとも言えない） | 62 | 31% |
| 4（満足） | 56 | 28% |
| 5（とても満足） | 30 | 15% |
| 合計 | 200 | 100％ |
集計表を作成する大きな目的はもちろん回答傾向を把握することですが、もう一つの目的はデータの入力ミスを防ぐことです。たとえば回答者が200人であったにもかかわらず、上の表の合計人数が199人となっていたら、一人の回答がうまく入力されていない可能性があります。その場合、データ表を見返して、なぜ200人になっていないのか確認する必要があります。
各質問の回答傾向を把握するとともに、データの入力ミスがないか、この段階で丁寧にチェックしていきます。
また、アンケート調査では少ないですが、回答結果が身長や体重などの連続データ（計量値）の場合があります。この場合の集計は、次のような度数分布表を作成することができます。
| 身長 | 人数 | 割合 |
|---|---|---|
| 145〜150 cm | 4 | 2％ |
| 150〜155 cm | 10 | 5% |
| 155〜160 cm | 28 | 14% |
| 160〜165 cm | 40 | 20% |
| 165〜170 cm | 44 | 22% |
| 170〜175 cm | 32 | 16% |
| 175〜180 cm | 24 | 12％ |
| 180〜185 cm | 14 | 7％ |
| 185〜190 cm | 4 | 2％ |
| 合計 | 200 | 100％ |
統計量を計算する
回答結果が連続データ（計量値）の場合は、次のような統計量を計算します。
統計量
平均値・中央値・標準偏差・最大値・最小値・範囲・25パーセンタイル・75パーセンタイル・四分位範囲・四分位偏差
ただし、これらのすべてを毎回計算する必要はなく、重要なものだけ計算して、データの全体像をつかめるようにしておきます。たとえば、データが正規分布している場合は平均値や標準偏差が、正規分布していない場合は中央値や最大値・最小値が重要になってきます。データの正規性についてこちらの記事をご覧ください。
論文を書くための統計解析：データの正規性とは？
計数データ（重さ、長さ、速度、個数など）の統計解析は、基本的にデータが正規分布していることが前提条件となります。グループ間を比較するにしても相関関係を調べるに…
棒グラフを作成する
集計表を作成して「回答傾向を把握する」と書きましたが、傾向を把握するためには表よりもグラフ（図）のほうが適しています。数字の大小を視覚的にとらえることができるからです。
人数（度数）は棒グラフ（連続データの場合はヒストグラム）を使って視覚化します。棒グラフは多くの方がイメージできると思うので、ここでは省略します。
帯グラフを作成する
アンケート調査結果の分析では、人数（度数）よりも割合が重要になることが多いはずです。たとえば、質問1には200人が回答したけれども、質問2には180人しか回答しなかった場合、選択肢1を選んだ人が同じ20人だったとしても、その意味は異なります。質問1では10％（=20/200）の回答者が、質問2では11%（=20/180）の回答者が選択肢1を選んだことになるからです。
そこで、人数ではなく、割合に注目した帯グラフを作成します。
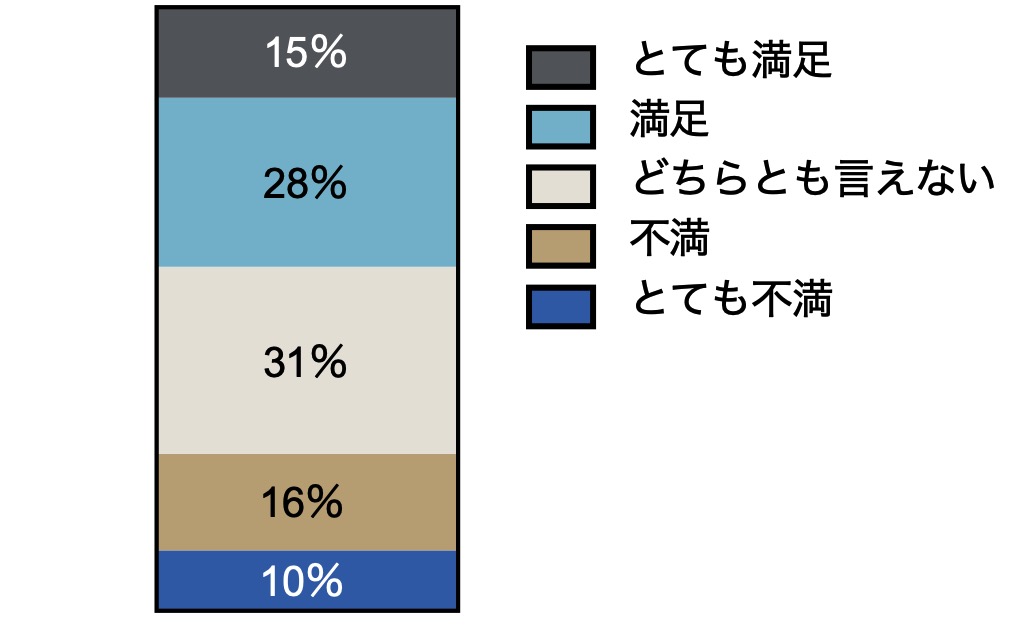
基準値と比較する
集計表や帯グラフが作成できれば、その回答傾向（割合の分布）を基準値と統計学的に比較することができます。ここでいう「基準値」とは、たとえば理論的に分かっている割合の分布や、過去の調査結果から得られた割合、目標としている割合など、何でもOKです。ある割合を基準としたときに、今回の調査で観測された割合が統計学的に有意に異なるかどうかを判断します。アンケート質問の数がたとえ1個だったとしても、回答結果が基準値から外れているかいないかを統計学的に調べられるということです。
統計解析の方法は、アンケートデータの種類によって変わってきます。上の表のように、1〜5のような順序尺度の場合（あるいは正規分布とみなせない連続尺度の場合）はコルモゴロフ・スミルノフ検定、名義尺度の場合はカイ二乗検定、正規分布とみなせる連続尺度の場合は1試料のt検定などを使用します。それぞれの解析方法については、自分が使っている統計ソフトで確認してください。
まとめ
今回の記事では、アンケート調査の結果を分析する最初のステップとして、
- 集計表にまとめる
- グラフを作成する
- 基準値と比較する
ということを紹介しました。次回はこの次のステップとして、二つの質問の間に関連があるかどうか調べる方法について解説します。
この記事を書いた人
田中泰章 博士
Yasuaki Tanaka Ph.D.
プロフィール
環境問題や教育制度などについて広い視点から考える自然科学者。2008年に東京大学大学院で博士号（環境学）を取得した後、東京大学、琉球大学、米国オハイオ州立大学、ブルネイ大学など、国内外の大学で研究と教育に約15年間携わってきました。これまでに30報以上の学術論文を筆頭著者として執筆し、国際的な科学雑誌の査読者として多数の論文審査も行っています。
