スピアマンの順位相関係数：使える場面と論文での書き方

前回の記事では、単回帰分析について解説しました。今回は、単回帰分析のノンパラメトリック版とも言える、スピアマンの順位相関（Spearman's rank correlation）について解説します。単回帰分析よりも多くの場面で使えるので、非常に便利な解析方法です。

単回帰分析の基本：エクセル出力結果の見方と論文での書き方

単回帰分析をエクセルで実行したときに出力される結果（分散分析表や回帰係数の有意性など）の見方や、論文での書き方などについて解説していきます。統計解析でお悩みの…

論文・研究相談サービス｜アカデミックラウンジ

どんなときに使える？

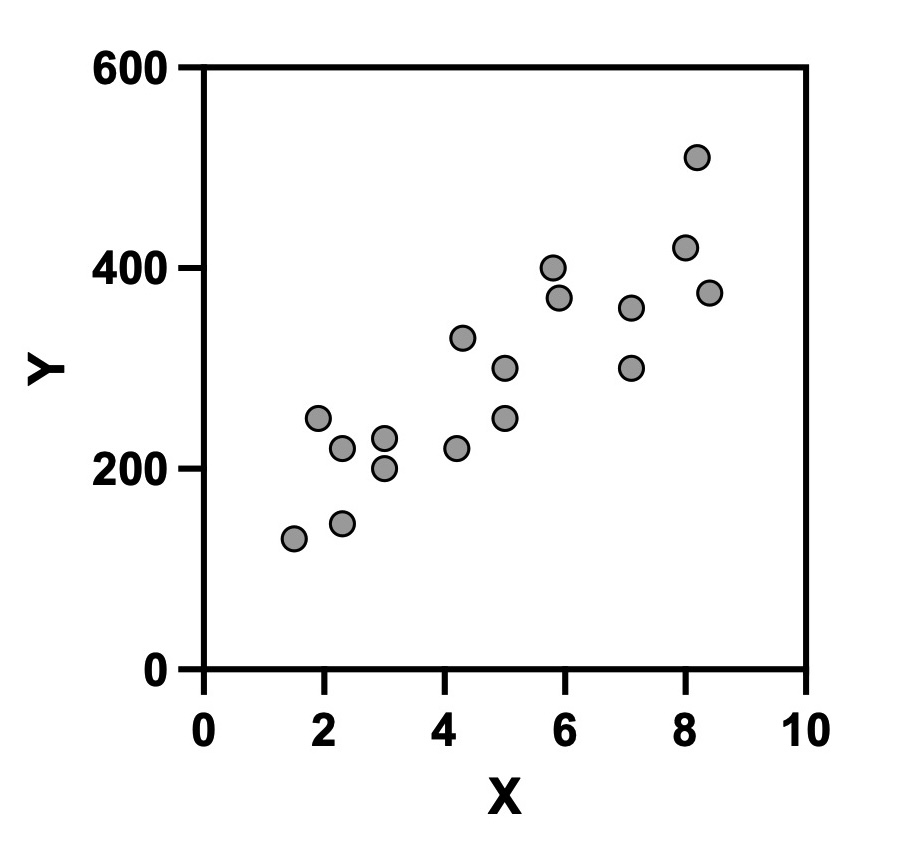
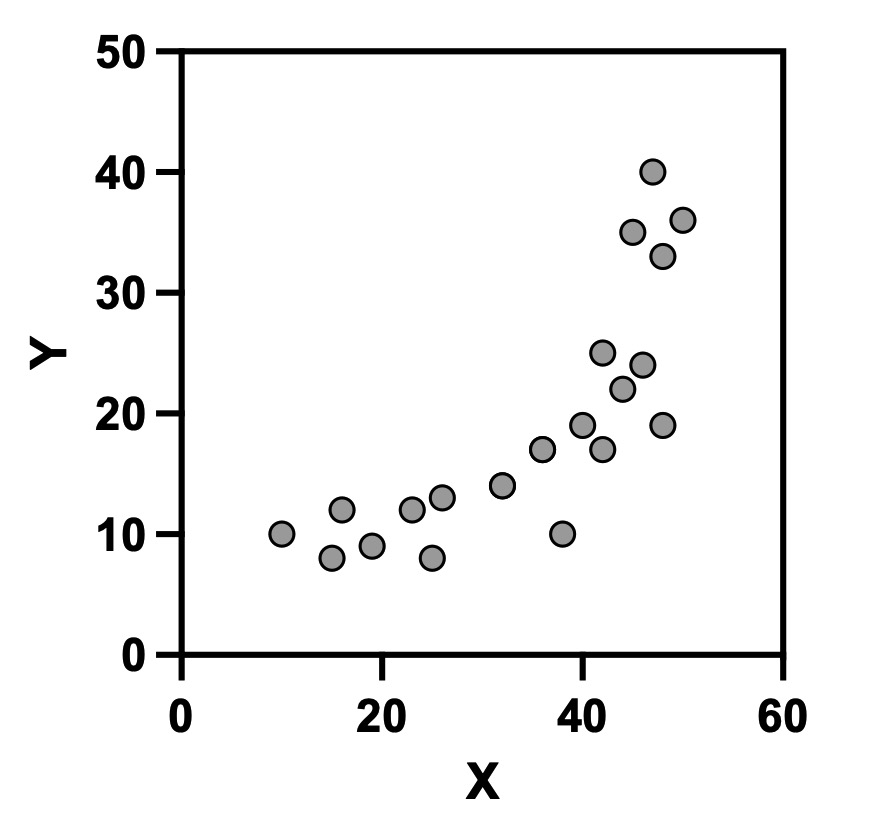
まず、スピアマンの順位相関がどういう場面で使えるのか、イメージできるようにしておきましょう。図1と図2の散布図を見てみてください。図1では、Xが増加するにつれてYが直線的に増加していることが分かります。それに対して図2では、Xが増加するとYも増加する傾向があるものの、直線的に増加しているわけではなさそうです。このように、直線的ではないけれど、目的変数が単調に増加（あるいは減少）しているように見えるときに、スピアマンの順位相関係数を使って、その増加（あるいは減少）が統計学的に有意かどうかを検証します。

単回帰分析より適用範囲が広い

直線を当てはめる単回帰分析では、回帰式の有意性を示すためには残差の正規性や等分散性など、いくつかの前提条件をクリアする必要があります。それに対してスピアマンの順位相関では、残差の正規性や等分散性などは求められないため、単回帰分析より広い範囲で利用することができます。

正規性や等分散性が求められないということは、数量データ（図1や図2のような数値データ）だけでなく、順序尺度でも利用できるということです。例えば、選択式アンケートの結果（順序尺度）は単回帰分析を実施できないことが多いので、スピアマンの順位相関係数を使ってデータの傾向を解析します。

解析結果の見方と記述方法

スピアマンの順位相関係数を使った検定結果は、単回帰分析に比べると非常にシンプルです。統計ソフトを使えば、相関係数とp値が出力されると思いますので、それらを見て有意性を判定します。

相関係数が正の値のときは、説明変数と目的変数に正の相関があることを示し、逆に負の値のときは、説明変数と目的変数に負の相関があることを示します。そして、一般的にはp値が0.05未満のとき、それらの相関が統計学的に有意と判定します。

図2の散布図を解析した結果、相関係数は0.86、p値は0.0001未満でしたので、次のように記述することができます。

解析結果の解釈（考察）

解析結果を解釈する方法は、単回帰分析の場合と同様です。有意な相関が見られたからといって、因果関係が示されたわけではありませんので、「（説明変数）が（目的変数）に影響を与えていることが分かった」というような記述は避けましょう。詳しくは単回帰分析の記事をご覧ください。

単回帰分析の基本：エクセル出力結果の見方と論文での書き方

単回帰分析をエクセルで実行したときに出力される結果（分散分析表や回帰係数の有意性など）の見方や、論文での書き方などについて解説していきます。統計解析でお悩みの…

論文・研究相談サービス｜アカデミックラウンジ

まとめ

スピアマンの順位相関係数を使った解析について、簡単に解説しました。

目的変数が数量データの場合、まずは単回帰分析を行ってみて、前提条件を満たさないときに順位相関を考えることになります。つまり、全体としては以下のような流れです。

1. 散布図を描いて、説明変数と目的変数が直線関係にあるかどうかチェックする。
2. 散布図に直線関係が見られる場合、単回帰分析を試みる（単回帰分析の前提条件を満たすならそのまま単回帰分析、満たさない場合はスピアマンの順位相関）。
3. 散布図に直線関係が見られない場合、スピアマンの順位相関を試みる。

目的変数が順序尺度の場合は、最初からスピアマンの順位相関を考えれば良いでしょう。

サービス案内

---